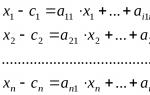Një shembull i një modeli matematikor. Përkufizimi, klasifikimi dhe veçoritë

Shembulli 1.5.1.

Lëreni një rajon të caktuar ekonomik të prodhojë disa (n) lloje produktesh ekskluzivisht më vete dhe vetëm për popullsinë e këtij rajoni. Supozohet se procesi teknologjik është përpunuar dhe kërkesa e popullsisë për këto mallra është studiuar. Është e nevojshme të përcaktohet vëllimi vjetor i prodhimit të produktit, duke marrë parasysh faktin se ky vëllim duhet të sigurojë si konsumin përfundimtar ashtu edhe atë industrial.

Le të krijojmë një model matematikor të këtij problemi. Sipas kushteve të tij jepen: llojet e produkteve, kërkesa për to dhe procesi teknologjik; ju duhet të gjeni vëllimin e prodhimit të secilit lloj produkti.

Le të shënojmë sasitë e njohura:

c i– kërkesa e popullsisë për i produktit ( i=1,...,n); a ij- sasi i produkti i kërkuar për të prodhuar një njësi të produktit të j-të duke përdorur një teknologji të caktuar ( i=1,...,n ; j=1,...,n);

X i – vëllimi i daljes i- produktit ( i=1,...,n); tërësia Me =(c 1 ,..., c n ) quhet vektori i kërkesës, numra a ij– koeficientët teknologjikë, dhe tërësia X =(X 1 ,..., X n ) – vektori i lëshimit.

Sipas kushteve problemore, vektori X shpërndahet në dy pjesë: për konsum final (vektor Me ) dhe për riprodhim (vektor x-s ). Le të llogarisim atë pjesë të vektorit X e cila shkon në riprodhim. Sipas përcaktimeve tona për prodhim X j sasia e produktit të j-të të furnizuar a ij · X j sasive i-produkti.

Pastaj shuma a i1 · X 1 +...+ a në · X n tregon atë vlerë i-produkti, i cili nevojitet për të gjithë lëshimin X =(X 1 ,..., X n ).

Prandaj, barazia duhet të plotësohet:

Duke e shtrirë këtë arsyetim në të gjitha llojet e produkteve, arrijmë në modelin e dëshiruar:

Zgjidhja e këtij sistemi prej n ekuacionesh lineare për X 1 ,...,X n dhe gjeni vektorin e kërkuar të lëshimit.

Për ta shkruar këtë model në një formë më kompakte (vektoriale), ne prezantojmë shënimin e mëposhtëm:

katror (
) -matricë A quhet matrica e teknologjisë. Është e lehtë të kontrollosh që modeli ynë tani do të shkruhet kështu: x-s=Ah ose

(1.6)

Ne morëm modelin klasik " Hyrje dalje “, autor i së cilës është ekonomisti i njohur amerikan V. Leontiev.

Shembulli 1.5.2.

Rafineria e naftës ka dy shkallë nafte: grade A në masën 10 njësi, nota NË- 15 njësi. Gjatë përpunimit të naftës, fitohen dy materiale: benzina (shënojmë B) dhe naftë ( M). Ekzistojnë tre opsione për procesin e teknologjisë së përpunimit:

I: 1 njësi A+ 2 njësi NË jep 3 njësi. B+ 2 njësi M

II: 2 njësi. A+ 1 njësi NË jep 1 njësi. B+ 5 njësi M

III: 2 njësi A+ 2 njësi NË jep 1 njësi. B+ 2 njësi M

Çmimi i benzinës është 10 dollarë për njësi, nafta është 1 dollarë për njësi.

Është e nevojshme të përcaktohet kombinimi më i favorshëm i proceseve teknologjike për përpunimin e sasisë së disponueshme të naftës.

Përpara modelimit, le të sqarojmë pikat e mëposhtme. Nga kushtet e problemit rezulton se “përfitueshmëria” e procesit teknologjik për uzinën duhet të kuptohet në kuptimin e përfitimit të të ardhurave maksimale nga shitja e produkteve të gatshme të saj (benzina dhe mazut). Në këtë drejtim, është e qartë se “zgjedhja (marrja) e vendimit” të uzinës konsiston në përcaktimin se cila teknologji do të aplikohet dhe sa herë. Natyrisht, ka mjaft opsione të tilla të mundshme.

Le të shënojmë sasitë e panjohura:

X i- sasia e përdorimit i procesi teknologjik (i=1,2,3). Parametra të tjerë të modelit (rezervat e naftës, çmimet e benzinës dhe naftës) i njohur.

Tani një vendim specifik për bimën zbret në zgjedhjen e një vektori X =(x 1 , X 2 , X 3 ) , për të cilat të ardhurat e uzinës janë të barabarta me (32x 1 +15x 2 +12x 3 ) dollarë Këtu, 32 dollarë janë të ardhurat e marra nga një aplikim i procesit të parë teknologjik ($10 3 njësi. B+ 1 dollar · 2 njësi. M= 32 dollarë). Koeficientët 15 dhe 12 për proceset e dyta dhe të treta teknologjike, përkatësisht, kanë një kuptim të ngjashëm. Kontabilizimi i rezervave të naftës çon në kushtet e mëposhtme:

për shumëllojshmëri A:

për shumëllojshmëri NË:,

ku në koeficientët e parë të pabarazisë 1, 2, 2 janë normat e konsumit të vajit të klasës A për përdorim një herë të proceseve teknologjike I,II,III përkatësisht. Koeficientët e pabarazisë së dytë kanë një kuptim të ngjashëm për vajin e klasës B.

Modeli matematik në tërësi ka formën:

Gjeni një vektor të tillë x = (x 1 , X 2 , X 3 ) për të maksimizuar

f(x) =32x 1 +15x 2 +12x 3

subjekt i kushteve të mëposhtme:

Forma e shkurtuar e kësaj hyrjeje është:

nën kufizime

(1.7)

Ne morëm të ashtuquajturin problem të programimit linear.

Modeli (1.7.) është një shembull i një modeli optimizimi të një tipi deterministik (me elementë të mirëpërcaktuar).

Shembulli 1.5.3.

Një investitor duhet të përcaktojë përzierjen më të mirë të aksioneve, obligacioneve dhe letrave të tjera me vlerë për të blerë për një shumë të caktuar në mënyrë që të marrë një fitim të caktuar me rrezik minimal për veten e tij. Fitimi për dollar të investuar në një letër me vlerë j- lloji, i karakterizuar nga dy tregues: fitimi i pritur dhe fitimi aktual. Për një investitor, është e dëshirueshme që fitimi i pritur për dollar investim të mos jetë më i ulët se një vlerë e dhënë për të gjithë grupin e letrave me vlerë. b.

Vini re se për të modeluar saktë këtë problem, një matematikan kërkohet të ketë njohuri të caktuara bazë në fushën e teorisë së portofolit të letrave me vlerë.

Le të shënojmë parametrat e njohur të problemit:

n– numri i llojeve të letrave me vlerë; A j– fitimi aktual (numër i rastësishëm) nga lloji j i letrës me vlerë; – fitimi i pritur nga j-lloji i sigurisë.

Le të shënojmë sasitë e panjohura :

y j - fondet e alokuara për blerjen e letrave me vlerë të këtij lloji j.

Duke përdorur shënimin tonë, e gjithë shuma e investuar shprehet si . Për të thjeshtuar modelin, ne prezantojmë sasi të reja

.

Kështu, X i- kjo është pjesa e të gjitha fondeve të alokuara për blerjen e letrave me vlerë të këtij lloji j.

Është e qartë se

Nga kushtet e problemit është e qartë se qëllimi i investitorit është të arrijë një nivel të caktuar fitimi me rrezik minimal. Në thelb, rreziku është një masë e devijimit të fitimit aktual nga ai i pritur. Prandaj, mund të identifikohet me kovariancën e fitimeve për letrat me vlerë të tipit i dhe tipit j. Këtu M është përcaktimi i pritjes matematikore.

Modeli matematikor i problemit origjinal ka formën:

nën kufizime

,
,
,
. (1.8)

Ne kemi marrë modelin e njohur Markowitz për optimizimin e strukturës së një portofoli letrash me vlerë.

Modeli (1.8.) është një shembull i një modeli optimizimi të tipit stokastik (me elemente të rastësisë).

Shembulli 1.5.4.

Në bazë të një organizate tregtare ekzistojnë n lloje të një prej produkteve të asortimentit minimal. Vetëm një lloj i një produkti të caktuar duhet të sillet në dyqan. Ju duhet të zgjidhni llojin e produktit që është i përshtatshëm për ta sjellë në dyqan. Nëse lloji i produktit j do të jetë në kërkesë, dyqani do të bëjë një fitim nga shitja e tij R j, nëse nuk është në kërkesë - një humbje q j .

Para modelimit, ne do të diskutojmë disa pika themelore. Në këtë problem, vendimmarrësi (DM) është dyqani. Sidoqoftë, rezultati (fitimi maksimal) varet jo vetëm nga vendimi i tij, por edhe nga fakti nëse produkti i importuar do të jetë në kërkesë, domethënë nëse do të blihet nga popullata (supozohet se për ndonjë arsye dyqani nuk e bën kanë mundësi të studiojnë kërkesën e popullsisë ). Prandaj, popullsia mund të konsiderohet si një vendimmarrës i dytë, duke zgjedhur llojin e produktit sipas preferencave të tyre. “Vendimi” më i keq i popullatës për një dyqan është: “Mallrat e importuara nuk janë të kërkuara”. Pra, për të marrë parasysh të gjitha situatat e mundshme, dyqani duhet të konsiderojë popullsinë si "armikun" e tij (me kusht), duke ndjekur qëllimin e kundërt - të minimizojë fitimin e dyqanit.

Pra, kemi një problem vendimmarrjeje me dy pjesëmarrës që ndjekin qëllime të kundërta. Le të sqarojmë se dyqani zgjedh një nga llojet e mallrave për shitje (ka n opsione vendimi), dhe popullsia zgjedh një nga llojet e mallrave që është në kërkesë më të madhe ( n opsionet e zgjidhjes).

Për të përpiluar një model matematikor, le të vizatojmë një tabelë me n linjat dhe n kolona (gjithsej n 2 qelizat) dhe bien dakord që rreshtat korrespondojnë me zgjedhjen e dyqanit, dhe kolonat me zgjedhjen e popullatës. Pastaj qeliza (i, j) korrespondon me situatën kur dyqani zgjedh i lloji i produktit ( i rreshti -th), dhe popullsia zgjedh j lloji i produktit ( j- kolona e th). Në secilën qelizë ne shkruajmë një vlerësim numerik (fitim ose humbje) të situatës përkatëse nga pikëpamja e dyqanit:

Numrat q i shkruar me një minus për të pasqyruar humbjen e dyqanit; në çdo situatë, “fitimi” i popullsisë (me kusht) është i barabartë me “fitimin” e dyqanit, marrë me shenjën e kundërt.

Një formë e shkurtuar e këtij modeli është:

(1.9)

Ne morëm të ashtuquajturën lojë matrice. Modeli (1.9.) është një shembull i modeleve të vendimmarrjes së lojës.

Baza për zgjidhjen e problemeve ekonomike janë modelet matematikore.

Modeli matematik problemi është një grup marrëdhëniesh matematikore që përshkruajnë thelbin e problemit.

• përzgjedhja e variablave të problemit
• hartimi i një sistemi kufizimesh
• zgjedhja e funksionit objektiv

Variablat e detyrave quhen sasitë X1, X2, Xn, të cilat karakterizojnë plotësisht procesin ekonomik. Zakonisht shkruhen si vektor: X=(X 1, X 2,...,X n).

Sistemi i kufizimeve problemet janë një grup ekuacionesh dhe pabarazish që përshkruajnë burimet e kufizuara në problemin në shqyrtim.

Funksioni objektiv detyrat quhen një funksion i variablave të detyrës që karakterizon cilësinë e detyrës dhe ekstremi i së cilës duhet të gjendet.

Në përgjithësi, një problem i programimit linear mund të shkruhet si më poshtë:

Kjo hyrje nënkupton sa më poshtë: gjeni ekstremin e funksionit objektiv (1) dhe variablat përkatëse X=(X 1 , X 2 ,...,X n) me kusht që këto variabla të plotësojnë sistemin e kufizimeve (2) dhe kushtet jonegative (3) .

Zgjidhje e vlefshme(plani) i problemit të programimit linear është çdo vektor n-dimensional X=(X 1 , X 2 ,...,X n) që plotëson sistemin e kufizimeve dhe kushteve jonegative.

Tërësia e zgjidhjeve (planeve) të realizueshme të formave të problemit rajoni i zgjidhjeve të realizueshme(ODR).

Zgjidhja optimale(plani) i një problemi të programimit linear është një zgjidhje (plan) e tillë e pranueshme e problemit në të cilën funksioni objektiv arrin një ekstrem.

Shembull i përpilimit të një modeli matematikor

Problemi i përdorimit të burimeve (lëndëve të para)

Gjendja: Për të prodhuar n lloje produktesh, përdoren m lloje burimesh. Krijoni një model matematikor.

E njohur:

• b i (i = 1,2,3,...,m) - rezervat e çdo lloji të i-të të burimit;
• a ij (i = 1,2,3,...,m; j=1,2,3,...,n) - kostot e çdo lloji të i-të burimi për prodhimin e një njësie vëllimi i llojit j të produktit;
• c j (j = 1,2,3,...,n) - fitimi nga shitja e një njësie vëllimi të llojit j të produktit.

Kërkohet hartimi i një plani prodhimi që siguron fitim maksimal sipas kufizimeve të dhëna mbi burimet (lëndët e para).

Zgjidhja:

Le të prezantojmë një vektor të ndryshoreve X=(X 1, X 2,...,X n), ku x j (j = 1,2,...,n) është vëllimi i prodhimit të tipit j të produkt.

Kostot e llojit të i-të të burimit për prodhimin e një vëllimi të caktuar x j të produkteve janë të barabarta me një ij x j, prandaj kufizimi në përdorimin e burimeve për prodhimin e të gjitha llojeve të produkteve ka formën:
Fitimi nga shitja e llojit j të produktit është i barabartë me c j x j, pra funksioni objektiv është i barabartë me:

Përgjigju- Modeli matematik duket si ky:

Forma kanonike e problemit të programimit linear

Në rastin e përgjithshëm, një problem i programimit linear shkruhet në atë mënyrë që kufizimet të jenë edhe ekuacione edhe pabarazi, dhe variablat mund të jenë ose jo-negativë ose të ndryshojnë në mënyrë arbitrare.

Në rastin kur të gjitha kufizimet janë ekuacione dhe të gjitha variablat plotësojnë kushtin e jonegativitetit, problemi i programimit linear quhet kanonike.

Mund të përfaqësohet në shënime koordinative, vektoriale dhe matricore.

Problemi i programimit linear kanonik në shënimin koordinativ ka formën:

Problemi kanonik i programimit linear në shënimin e matricës ka formën:

• A është matrica e koeficientëve të sistemit të ekuacioneve
• X-matrica-kolona e variablave të detyrës
• Ао - matricë-kolona e pjesëve të djathta të sistemit të kufizimeve

Shpesh përdoren problemet e programimit linear, të quajtura simetrike, të cilat në shënimin e matricës kanë formën:

Reduktimi i një problemi të përgjithshëm të programimit linear në formë kanonike

Në shumicën e metodave për zgjidhjen e problemeve të programimit linear, supozohet se sistemi i kufizimeve përbëhet nga ekuacione dhe kushte natyrore për mosnegativitetin e variablave. Megjithatë, gjatë përpilimit të modeleve të problemeve ekonomike, kufizimet formohen kryesisht në formën e një sistemi pabarazish, kështu që është e nevojshme të mund të kalojmë nga një sistem pabarazish në një sistem ekuacionesh.

Le të marrim pabarazinë lineare a 1 x 1 +a 2 x 2 +...+a n x n ≤b dhe të shtojmë në anën e majtë një vlerë të caktuar x n+1 të tillë që pabarazia të kthehet në barazi a 1 x 1 +a 2 x 2 + ...+a n x n +x n+1 =b. Për më tepër, kjo vlerë x n+1 është jo negative.

Le të shohim gjithçka duke përdorur një shembull.

Sillni problemin e programimit linear në formën kanonike:

Zgjidhja:
Le të kalojmë në problemin e gjetjes së maksimumit të funksionit objektiv.
Për ta bërë këtë, ne ndryshojmë shenjat e koeficientëve të funksionit objektiv.
Për të transformuar pabarazitë e dytë dhe të tretë të sistemit të kufizimeve në ekuacione, ne prezantojmë ndryshore shtesë jo negative x 4 x 5 (në modelin matematikor ky veprim shënohet me shkronjën D).
Ndryshorja x 4 futet në anën e majtë të pabarazisë së dytë me shenjën "+", pasi pabarazia ka formën "≤".
Ndryshorja x 5 futet në anën e majtë të pabarazisë së tretë me shenjën "-", pasi pabarazia ka formën "≥".
Variablat x 4 x 5 futen në funksionin objektiv me një koeficient. e barabartë me zero.
Ne e shkruajmë problemin në formë kanonike.

Çfarë është një model matematikor?

Koncepti i një modeli matematikor.

Një model matematikor është një koncept shumë i thjeshtë. Dhe shumë e rëndësishme. Janë modelet matematikore që lidhin matematikën dhe jetën reale.

Me fjalë të thjeshta, një model matematikor është një përshkrim matematikor i çdo situate. Kjo eshte e gjitha. Modeli mund të jetë primitiv, ose mund të jetë super kompleks. Sido që të jetë situata, i tillë është modeli.)

Në çdo (e përsëris - ne cdo!) në një rast kur duhet të numëroni dhe llogaritni diçka - ne jemi të angazhuar në modelimin matematik. Edhe nëse nuk e dyshojmë.)

P = 2 CB + 3 CM

Kjo hyrje do të jetë një model matematikor i kostove të blerjeve tona. Modeli nuk merr parasysh ngjyrën e paketimit, datën e skadencës, mirësjelljen e arkëtarëve etj. Kjo është arsyeja pse ajo model, jo një blerje reale. Por shpenzimet, d.m.th. çfarë kemi nevojë- do ta zbulojmë me siguri. Nëse modeli është i saktë, sigurisht.

Është e dobishme të imagjinohet se çfarë është një model matematikor, por nuk mjafton. Gjëja më e rëndësishme është të jeni në gjendje të ndërtoni këto modele.

Hartimi (ndërtimi) i një modeli matematikor të problemës.

Të krijosh një model matematikor do të thotë të përkthesh kushtet e problemit në formë matematikore. Ato. kthejnë fjalët në ekuacion, formulë, pabarazi etj. Për më tepër, transformojeni atë në mënyrë që kjo matematikë të korrespondojë rreptësisht me tekstin burimor. Përndryshe, do të përfundojmë me një model matematikor të një problemi tjetër të panjohur për ne.)

Më konkretisht, keni nevojë

Ka një numër të pafund detyrash në botë. Prandaj, ofroni udhëzime të qarta hap pas hapi për hartimin e një modeli matematikor ndonjë detyrat janë të pamundura.

Por ka tre pika kryesore që duhet t'i kushtoni vëmendje.

1. Çdo problem përmban tekst, çuditërisht.) Ky tekst, si rregull, përmban informacion i qartë, i hapur. Numrat, vlerat, etj.

2. Çdo problem ka informacione të fshehura. Ky është një tekst që supozon njohuri shtesë në kokën tuaj. Nuk ka rrugë pa to. Përveç kësaj, informacioni matematikor shpesh fshihet pas fjalëve të thjeshta dhe... rrëshqet vëmendjen.

3. Çdo detyrë duhet dhënë lidhja e të dhënave me njëra-tjetrën. Kjo lidhje mund të jepet në tekst të thjeshtë (diçka është e barabartë me diçka), ose mund të fshihet pas fjalëve të thjeshta. Por faktet e thjeshta dhe të qarta shpesh anashkalohen. Dhe modeli nuk është përpiluar në asnjë mënyrë.

Unë do të them menjëherë: për të zbatuar këto tre pika, duhet ta lexoni problemin (dhe me kujdes!) disa herë. Gjëja e zakonshme.

Dhe tani - shembuj.

Le të fillojmë me një problem të thjeshtë:

Petrovich u kthye nga peshkimi dhe me krenari prezantoi kapjen e tij para familjes. Pas ekzaminimit më të afërt, rezultoi se 8 peshq vinin nga detet veriore, 20% e të gjithë peshqve vinin nga detet jugore dhe asnjë i vetëm nuk vinte nga lumi lokal ku Petrovich po peshkonte. Sa peshq bleu Petrovich në dyqanin e detit?

Të gjitha këto fjalë duhet të kthehen në një lloj ekuacioni. Për ta bërë këtë ju duhet, e përsëris, vendos një lidhje matematikore midis të gjitha të dhënave në problem.

Ku të fillojë? Së pari, le të nxjerrim të gjitha të dhënat nga detyra. Le të fillojmë me radhë:

Le t'i kushtojmë vëmendje pikës së parë.

Cili është këtu? eksplicite informacion matematikor? 8 peshq dhe 20%. Jo shumë, por nuk na duhen shumë.)

Le t'i kushtojmë vëmendje pikës së dytë.

Kërkojnë i fshehur informacion. Eshte ketu. Këto janë fjalët: “20% e të gjithë peshqve“Këtu duhet të kuptosh se sa janë përqindjet dhe si llogariten, përndryshe nuk zgjidhet problemi, pikërisht ky është informacioni shtesë që duhet të kesh në kokë.

Ka edhe matematikore informacion që është plotësisht i padukshëm. Kjo pyetje detyre: "Sa peshk bleva..." Ky është gjithashtu një numër. Dhe pa të, nuk do të formohet asnjë model. Prandaj, le ta shënojmë këtë numër me shkronjë "X". Ne ende nuk e dimë se çfarë është e barabartë me x, por ky përcaktim do të jetë shumë i dobishëm për ne. Më shumë detaje se çfarë duhet marrë për X dhe si ta trajtojmë atë janë shkruar në mësimin Si të zgjidhim problemet në matematikë? Le ta shkruajmë menjëherë:

x copa - numri i përgjithshëm i peshkut.

Në problemin tonë, peshqit e jugut janë dhënë në përqindje. Ne duhet t'i kthejmë ato në copa. Per cfare? Pastaj çfarë në ndonjë duhet hartuar problemi i modelit në të njëjtat lloj sasish. Copa - kështu që gjithçka është në copa. Nëse jepen, le të themi, orë dhe minuta, ne përkthejmë gjithçka në një gjë - ose vetëm orë, ose vetëm minuta. Nuk ka rëndësi se çfarë është. Është e rëndësishme që të gjitha vlerat ishin të të njëjtit lloj.

Le të kthehemi te zbulimi i informacionit. Kush nuk e di se çfarë është përqindja, nuk do ta zbulojë kurrë, po... Por kush e di do të thotë menjëherë se këtu përqindjet janë bazuar në numrin total të peshqve. Dhe ne nuk e dimë këtë numër. Asgjë nuk do të funksionojë!

Nuk është më kot që shënojmë numrin e përgjithshëm të peshkut (në copa!) "X" caktuar. Nuk do të jetë e mundur të numërohet numri i peshqve të jugut, por ne mund t'i shkruajmë ato? Si kjo:

0,2 x copa - numri i peshqve nga detet jugore.

Tani kemi shkarkuar të gjithë informacionin nga detyra. Edhe të dukshme edhe të fshehura.

Le t'i kushtojmë vëmendje pikës së tretë.

Kërkojnë lidhje matematikore ndërmjet të dhënave të detyrës. Kjo lidhje është aq e thjeshtë sa shumë nuk e vënë re... Kjo ndodh shpesh. Këtu është e dobishme thjesht të shkruani të dhënat e mbledhura në një grumbull dhe të shihni se çfarë është.

Çfarë kemi ne? Hani 8 copë peshk verior, 0,2 x copa- peshk jugor dhe x peshk- shuma totale. A është e mundur që këto të dhëna të lidhen disi? Po Lehtë! Numri i përgjithshëm i peshqve barazohet shuma e jugut dhe veriut! Epo, kush do ta kishte menduar...) Pra, ne e shkruajmë atë:

x = 8 + 0,2x

Ky është ekuacioni modeli matematikor i problemit tonë.

Ju lutemi vini re se në këtë problem Nuk na kërkohet të palosim asgjë! Ishim ne vetë, pa kokë, që kuptuam se shuma e peshqve të jugut dhe të veriut do të na jepte numrin total. Gjëja është aq e qartë sa kalon pa u vënë re. Por pa këto dëshmi, nuk mund të krijohet një model matematikor. Si kjo.

Tani mund të përdorni fuqinë e plotë të matematikës për të zgjidhur këtë ekuacion). Pikërisht për këtë u përpilua modeli matematik. Ne e zgjidhim këtë ekuacion linear dhe marrim përgjigjen.

Përgjigje: x=10

Le të krijojmë një model matematikor të një problemi tjetër:

Ata e pyetën Petroviçin: "A keni shumë para?" Petrovich filloi të qajë dhe u përgjigj: "Po, vetëm pak, nëse shpenzoj gjysmën e të gjitha parave dhe gjysmën e pjesës tjetër, atëherë do të më mbetet vetëm një thes me para ..." Sa para ka Petrovich. ?

Përsëri punojmë pikë për pikë.

1. Ne jemi duke kërkuar për informacion të qartë. Nuk do ta gjeni menjëherë! Informacioni i qartë është njëçantë me para. Ka disa gjysma të tjera... Epo, do ta shqyrtojmë këtë në paragrafin e dytë.

2. Ne jemi në kërkim të informacionit të fshehur. Këto janë gjysma. Çfarë? Jo shumë e qartë. Ne jemi duke kërkuar më tej. Ka edhe një pyetje: "Sa para ka Petrovich?" Le ta shënojmë shumën e parave me shkronjë "X":

X- të gjitha paratë

Dhe përsëri lexojmë problemin. Tashmë duke e ditur atë Petrovich X paratë. Këtu do të funksionojnë gjysmat! Ne shkruajmë:

0,5 x- gjysma e të gjitha parave.

Pjesa e mbetur do të jetë gjithashtu gjysma, d.m.th. 0,5 x. Dhe gjysma e gjysmës mund të shkruhet kështu:

0,5 0,5 x = 0,25x- gjysma e pjesës së mbetur.

Tani të gjitha informacionet e fshehura janë zbuluar dhe regjistruar.

3. Ne jemi duke kërkuar për një lidhje midis të dhënave të regjistruara. Këtu thjesht mund të lexoni vuajtjet e Petrovich dhe t'i shkruani matematikisht):

Nëse shpenzoj gjysmën e të gjitha parave...

Le ta regjistrojmë këtë proces. Të gjitha paratë - X. gjysma - 0,5 x. Të shpenzosh është të heqësh. Fraza kthehet në një regjistrim:

x - 0,5 x

po gjysma e pjesës tjetër...

Le të zbresim një gjysmë tjetër të pjesës së mbetur:

x - 0,5 x - 0,25x

atëherë do të më mbetet vetëm një thes me para...

Dhe këtu kemi gjetur barazi! Pas të gjitha zbritjeve, mbetet një thes me para:

x - 0,5 x - 0,25x = 1

Këtu është një model matematikor! Ky është përsëri një ekuacion linear, ne e zgjidhim atë, marrim:

Pyetje për shqyrtim. Çfarë është katër? Rubla, dollar, juan? Dhe në cilat njësi janë shkruar paratë në modelin tonë matematikor? Në çanta! Kjo do të thotë katër çantë para nga Petrovich. Mire gjithashtu.)

Detyrat janë, natyrisht, elementare. Kjo është veçanërisht për të kapur thelbin e hartimit të një modeli matematikor. Disa detyra mund të përmbajnë shumë më tepër të dhëna, të cilat mund të jenë të lehta për t'u humbur. Kjo ndodh shpesh në të ashtuquajturat. detyrat e kompetencës. Mënyra e nxjerrjes së përmbajtjes matematikore nga një grumbull fjalësh dhe numrash tregohet me shembuj

Një shënim më shumë. Në problemet klasike të shkollës (gypat që mbushin një pishinë, varkat që notojnë diku, etj.), Të gjitha të dhënat, si rregull, zgjidhen me shumë kujdes. Ka dy rregulla:
- ka informacion të mjaftueshëm në problem për ta zgjidhur atë,
- Nuk ka informacion të panevojshëm në një problem.

Kjo është një aluzion. Nëse ka mbetur ndonjë vlerë e papërdorur në modelin matematikor, mendoni nëse ka ndonjë gabim. Nëse nuk ka të dhëna të mjaftueshme, ka shumë të ngjarë, jo të gjitha informacionet e fshehura janë identifikuar dhe regjistruar.

Në detyrat e lidhura me kompetencat dhe detyrat e tjera të jetës, këto rregulla nuk respektohen rreptësisht. Asnjë e dhënë. Por edhe probleme të tilla mund të zgjidhen. Nëse, sigurisht, praktikoni në ato klasike.)

Nëse ju pëlqen kjo faqe...

Nga rruga, unë kam disa faqe më interesante për ju.)

Ju mund të praktikoni zgjidhjen e shembujve dhe të zbuloni nivelin tuaj. Testimi me verifikim të menjëhershëm. Le të mësojmë - me interes!)

Mund të njiheni me funksionet dhe derivatet.

MODEL MATEMATIK - paraqitje e një dukurie ose procesi të studiuar në njohuri konkrete shkencore në gjuhën e koncepteve matematikore. Në këtë rast, një sërë veçorish të fenomenit në studim pritet të përftohen nëpërmjet studimit të karakteristikave aktuale matematikore të modelit. Ndërtimi i M.m. më së shpeshti diktohet nga nevoja për të pasur një analizë sasiore të dukurive dhe proceseve që studiohen, pa të cilat, nga ana tjetër, është e pamundur të bëhen parashikime të verifikueshme eksperimentalisht për rrjedhën e tyre.

Procesi i modelimit matematik, si rregull, kalon nëpër fazat e mëposhtme. Në fazën e parë, identifikohen lidhjet midis parametrave kryesorë të M.m. Ne po flasim kryesisht për një analizë cilësore të fenomeneve në studim dhe formulimin e modeleve që lidhin objektet kryesore të kërkimit. Mbi këtë bazë, identifikohen objektet që mund të përshkruhen në mënyrë sasiore. Faza përfundon me ndërtimin e një modeli hipotetik, me fjalë të tjera, duke regjistruar në gjuhën e koncepteve matematikore ide cilësore për marrëdhëniet midis objekteve kryesore të modelit, të cilat mund të karakterizohen në mënyrë sasiore.

Në fazën e dytë studiohen problemet aktuale matematikore tek të cilat të çon modeli hipotetik i ndërtuar. Gjëja kryesore në këtë fazë është të përftohen pasoja teorike të verifikueshme empirikisht (zgjidhja e problemit të drejtpërdrejtë) si rezultat i analizës matematikore të modelit. Njëkohësisht, ka shpesh raste kur, për të ndërtuar dhe studiuar M.m. në fusha të ndryshme të njohurive konkrete shkencore, përdoret i njëjti aparat matematikor (për shembull, ekuacione diferenciale) dhe lindin probleme matematikore të të njëjtit lloj, megjithëse shumë jo të parëndësishme në çdo rast specifik. Për më tepër, në këtë fazë, përdorimi i kompjuterëve (kompjuterëve) me shpejtësi të lartë merr një rëndësi të madhe, gjë që bën të mundur marrjen e zgjidhjeve të përafërta të problemeve, shpesh të pamundura në kuadrin e matematikës së pastër, me një shkallë saktësie të paarritshme më parë ( pa përdorimin e kompjuterit).

Faza e tretë karakterizohet nga aktivitete për të identifikuar shkallën e përshtatshmërisë së M.M hipotetike të ndërtuar. ato dukuri dhe procese për të cilat synohej të studiohej. Domethënë, nëse të gjithë parametrat e modelit janë specifikuar, studiuesit përpiqen të zbulojnë se në çfarë mase, brenda kufijve të saktësisë së vëzhgimit, rezultatet e tyre janë në përputhje me pasojat teorike të modelit. Devijimet përtej kufijve të saktësisë së vëzhgimit tregojnë papërshtatshmërinë e modelit. Sidoqoftë, ka shpesh raste kur, kur ndërtohet një model, një numër i parametrave të tij mbeten

i pasigurt. Problemet në të cilat karakteristikat parametrike të modelit përcaktohen në mënyrë të tillë që pasojat teorike të jenë të krahasueshme, brenda kufijve të saktësisë së vëzhgimit, me rezultatet e testeve empirike quhen probleme inverse.

Në fazën e katërt, duke marrë parasysh identifikimin e shkallës së përshtatshmërisë së modelit hipotetik të ndërtuar dhe shfaqjen e të dhënave të reja eksperimentale mbi fenomenet në studim, ndodh analiza dhe modifikimi i mëvonshëm i modelit. Këtu vendimi i marrë varion nga refuzimi i pakushtëzuar i mjeteve matematikore të aplikuara deri te pranimi i modelit të ndërtuar si themeli për ndërtimin e një teorie thelbësisht të re shkencore.

Së pari M.m. u shfaq në shkencën e lashtë. Kështu, për të modeluar sistemin diellor, matematikani dhe astronomi grek Eudoxus i dha secilit planet katër sfera, kombinimi i lëvizjeve të të cilave krijoi një hipoped - një kurbë matematikore e ngjashme me lëvizjen e vëzhguar të planetit. Meqenëse, megjithatë, ky model nuk mund të shpjegonte të gjitha anomalitë e vëzhguara në lëvizjen e planetëve, ai u zëvendësua më vonë nga modeli epiciklik i Apollonit të Pergës. Modeli i fundit u përdor në studimet e tij nga Hipparchus, dhe më pas, pasi iu nënshtrua disa modifikimeve, nga Ptolemeu. Ky model, si paraardhësit e tij, bazohej në besimin se planetët i nënshtroheshin lëvizjeve rrethore uniforme, mbivendosja e të cilave shpjegonte parregullsitë e dukshme. Duhet të theksohet se modeli i Kopernikut ishte thelbësisht i ri vetëm në kuptimin cilësor (por jo si M.M.). Dhe vetëm Kepler, bazuar në vëzhgimet e Tycho Brahe, ndërtoi një M.M të ri. Sistemi diellor, duke vërtetuar se planetët nuk lëvizin në orbita rrethore, por në orbita eliptike.

Aktualisht, më të përshtatshmet konsiderohen të jenë ato të ndërtuara për të përshkruar dukuritë mekanike dhe fizike. Mbi mjaftueshmërinë e M.m. jashtë fizikës, me disa përjashtime, mund të flitet me mjaft kujdes. Megjithatë, fiksimi i natyrës hipotetike, dhe shpeshherë thjesht pamjaftueshmërisë së M.m. në fusha të ndryshme të dijes nuk duhet nënvlerësuar roli i tyre në zhvillimin e shkencës. Ka shpesh raste kur edhe modelet që janë larg të qenit adekuate kanë organizuar dhe stimuluar ndjeshëm kërkime të mëtejshme, së bashku me përfundime të gabuara që përmbanin edhe kokrra të vërteta që justifikonin plotësisht përpjekjet e shpenzuara për zhvillimin e këtyre modeleve.

Literatura:

Modelimi i matematikës. M., 1979;

Ruzavin G.I. Matematizimi i njohurive shkencore. M., 1984;

Tutubalin V.N., Barabasheva Yu.M., Grigoryan A.A., Devyatkova G.N., Uger E.G. Ekuacionet diferenciale në ekologji: reflektim historik dhe metodologjik // Pyetje të historisë së shkencës dhe teknologjisë natyrore. 1997. Nr. 3.

Fjalor i termave filozofikë. Botimi shkencor i Profesor V.G. Kuznetsova. M., INFRA-M, 2007, f. 310-311.

Modelimi i matematikës

1. Çfarë është modelimi matematik?

Nga mesi i shekullit të 20-të. Metodat matematikore dhe kompjuterët filluan të përdoren gjerësisht në fusha të ndryshme të veprimtarisë njerëzore. Janë shfaqur disiplina të reja si “ekonomia matematike”, “kimia matematike”, “gjuhësia matematikore” etj., duke studiuar modelet matematikore të objekteve dhe dukurive përkatëse, si dhe metodat e studimit të këtyre modeleve.

Një model matematikor është një përshkrim i përafërt i çdo klase fenomenesh ose objektesh të botës reale në gjuhën e matematikës. Qëllimi kryesor i modelimit është të eksplorojë këto objekte dhe të parashikojë rezultatet e vëzhgimeve të ardhshme. Megjithatë, modelimi është gjithashtu një metodë për të kuptuar botën përreth nesh, duke bërë të mundur kontrollin e saj.

Modelimi matematik dhe eksperimenti kompjuterik shoqërues janë të domosdoshëm në rastet kur një eksperiment në shkallë të plotë është i pamundur ose i vështirë për një arsye ose një tjetër. Për shembull, është e pamundur të vendosësh një eksperiment natyror në histori për të kontrolluar "çfarë do të kishte ndodhur nëse..." Është e pamundur të kontrollosh korrektësinë e një ose një tjetër teorie kozmologjike. Është e mundur, por nuk ka gjasa të jetë e arsyeshme, të eksperimentosh me përhapjen e një sëmundjeje, siç është murtaja, ose të kryesh një shpërthim bërthamor për të studiuar pasojat e saj. Megjithatë, e gjithë kjo mund të bëhet në një kompjuter duke ndërtuar fillimisht modele matematikore të dukurive që studiohen.

2. Fazat kryesore të modelimit matematik

1) Model ndërtimi. Në këtë fazë, specifikohet një objekt "jo matematikor" - një fenomen natyror, dizajn, plan ekonomik, proces prodhimi etj. Në këtë rast, si rregull, një përshkrim i qartë i situatës është i vështirë. Së pari, identifikohen tiparet kryesore të fenomenit dhe lidhjet ndërmjet tyre në nivel cilësor. Pastaj varësitë e gjetura cilësore formulohen në gjuhën e matematikës, domethënë ndërtohet një model matematikor. Kjo është faza më e vështirë e modelimit.

2) Zgjidhja e problemës matematikore në të cilën të çon modeli. Në këtë fazë i kushtohet shumë vëmendje zhvillimit të algoritmeve dhe metodave numerike për zgjidhjen e problemit në kompjuter, me ndihmën e të cilave mund të gjendet rezultati me saktësinë e kërkuar dhe brenda një kohe të pranueshme.

3) Interpretimi i pasojave të fituara nga modeli matematik. Pasojat e nxjerra nga modeli në gjuhën e matematikës interpretohen në gjuhën e pranuar në terren.

4) Kontrollimi i përshtatshmërisë së modelit. Në këtë fazë, përcaktohet nëse rezultatet eksperimentale përputhen me pasojat teorike të modelit brenda një saktësie të caktuar.

5) Modifikimi i modelit. Në këtë fazë, ose modeli është i ndërlikuar në mënyrë që të jetë më i përshtatshëm me realitetin, ose thjeshtohet për të arritur një zgjidhje praktikisht të pranueshme.

3. Klasifikimi i modeleve

Modelet mund të klasifikohen sipas kritereve të ndryshme. Për shembull, sipas natyrës së problemeve që zgjidhen, modelet mund të ndahen në funksionale dhe strukturore. Në rastin e parë, të gjitha sasitë që karakterizojnë një fenomen ose objekt shprehen në mënyrë sasiore. Për më tepër, disa prej tyre konsiderohen si variabla të pavarur, ndërsa të tjerët konsiderohen si funksione të këtyre sasive. Një model matematikor është zakonisht një sistem ekuacionesh të llojeve të ndryshme (diferenciale, algjebrike, etj.) që vendosin marrëdhënie sasiore midis sasive në shqyrtim. Në rastin e dytë, modeli karakterizon strukturën e një objekti kompleks të përbërë nga pjesë individuale, midis të cilave ka lidhje të caktuara. Në mënyrë tipike, këto lidhje nuk janë të matshme. Për të ndërtuar modele të tilla, është e përshtatshme të përdoret teoria e grafikut. Grafiku është një objekt matematikor që përfaqëson një grup pikash (kulme) në një rrafsh ose në hapësirë, disa prej të cilave janë të lidhura me vija (skajet).

Në bazë të natyrës së të dhënave dhe rezultateve fillestare, modelet e parashikimit mund të ndahen në përcaktuese dhe probabiliste-statistikore. Modelet e tipit të parë bëjnë parashikime të caktuara, të paqarta. Modelet e llojit të dytë bazohen në informacione statistikore, dhe parashikimet e marra me ndihmën e tyre janë të natyrës probabiliste.

4. Shembuj të modeleve matematikore

1) Probleme rreth lëvizjes së një predheje.

Merrni parasysh problemin e mëposhtëm të mekanikës.

Predha lëshohet nga Toka me një shpejtësi fillestare v 0 = 30 m/s në një kënd a = 45° në sipërfaqen e saj; kërkohet të gjendet trajektorja e lëvizjes së saj dhe distanca S ndërmjet pikës së fillimit dhe mbarimit të kësaj trajektoreje.

Pastaj, siç dihet nga një kurs i fizikës shkollore, lëvizja e një predhe përshkruhet me formulat:

ku t është koha, g = 10 m/s 2 është nxitimi i gravitetit. Këto formula ofrojnë një model matematikor të problemit. Duke shprehur t përmes x nga ekuacioni i parë dhe duke e zëvendësuar atë me të dytin, marrim ekuacionin për trajektoren e predhës:

Kjo kurbë (parabolë) pret boshtin x në dy pika: x 1 = 0 (fillimi i trajektores) dhe (vendi ku ka rënë predha). Duke zëvendësuar vlerat e dhëna të v0 dhe a në formulat që rezultojnë, marrim

përgjigje: y = x – 90x 2, S = 90 m.

Vini re se gjatë ndërtimit të këtij modeli, u përdorën një numër supozimesh: për shembull, supozohet se Toka është e sheshtë, dhe ajri dhe rrotullimi i Tokës nuk ndikojnë në lëvizjen e predhës.

2) Problemi për një rezervuar me sipërfaqen më të vogël.

Kërkohet të gjendet lartësia h 0 dhe rrezja r 0 e një rezervuari prej kallaji me vëllim V = 30 m 3, që ka formën e një cilindri rrethor të mbyllur, në të cilin sipërfaqja e saj S është minimale (në këtë rast, më së paku sasia e kallajit do të përdoret për prodhimin e tij).

Le të shkruajmë formulat e mëposhtme për vëllimin dhe sipërfaqen e një cilindri me lartësi h dhe rreze r:

V = p r 2 h, S = 2p r(r + h).

Duke shprehur h përmes r dhe V nga formula e parë dhe duke zëvendësuar shprehjen që rezulton në të dytën, marrim:

Kështu, nga pikëpamja matematikore, problemi zbret në përcaktimin e vlerës së r në të cilën funksioni S(r) arrin minimumin e tij. Le të gjejmë ato vlera të r 0 për të cilat derivati

shkon në zero: Mund të kontrolloni nëse derivati ​​i dytë i funksionit S(r) ndryshon shenjën nga minus në plus kur argumenti r kalon në pikën r 0 . Rrjedhimisht, në pikën r0 funksioni S(r) ka një minimum. Vlera përkatëse është h 0 = 2r 0 . Duke zëvendësuar vlerën e dhënë V në shprehjen për r 0 dhe h 0, marrim rrezen e dëshiruar dhe lartësia

3) Problemi i transportit.

Qyteti ka dy magazina mielli dhe dy furra buke. Nga magazina e parë transportohen çdo ditë 50 tonë miell dhe nga e dyta në fabrika 70 tonë, me 40 tonë në të parën dhe 80 tonë në të dytën.

Le të shënojmë me a ij është kostoja e transportit të 1 ton miell nga magazina e i-të në uzinën e j-të (i, j = 1,2). Le

a 11 = 1,2 rubla, a 12 = 1,6 rubla, a 21 = 0,8 fshij., a 22 = 1 fshij.

Si duhet planifikuar transporti në mënyrë që kostoja e tij të jetë minimale?

Le t'i japim problemit një formulim matematikor. Le të shënojmë me x 1 dhe x 2 sasinë e miellit që duhet të transportohet nga magazina e parë në fabrikën e parë dhe të dytë, dhe me x 3 dhe x 4 - nga magazina e dytë në fabrikën e parë dhe të dytë, përkatësisht. Pastaj:

x 1 + x 2 = 50, x 3 + x 4 = 70, x 1 + x 3 = 40, x 2 + x 4 = 80. (1)

Kostoja totale e të gjithë transportit përcaktohet nga formula

f = 1,2x 1 + 1,6x 2 + 0,8x 3 + x 4.

Nga pikëpamja matematikore, problemi është gjetja e katër numrave x 1, x 2, x 3 dhe x 4 që plotësojnë të gjitha kushtet e dhëna dhe japin minimumin e funksionit f. Le të zgjidhim sistemin e ekuacioneve (1) për xi (i = 1, 2, 3, 4) duke eliminuar të panjohurat. Ne e kuptojmë atë

x 1 = x 4 – 30, x 2 = 80 – x 4, x 3 = 70 – x 4, (2)

dhe x 4 nuk mund të përcaktohet në mënyrë unike. Meqenëse x i і 0 (i = 1, 2, 3, 4), nga ekuacionet (2) rrjedh se 30Ј x 4 Ј 70. Duke zëvendësuar shprehjen për x 1, x 2, x 3 në formulën për f, marrim

f = 148 - 0,2x 4.

Është e lehtë të shihet se minimumi i këtij funksioni arrihet në vlerën maksimale të mundshme prej x 4, domethënë në x 4 = 70. Vlerat përkatëse të të panjohurave të tjera përcaktohen nga formula (2): x 1 = 40, x 2 = 10, x 3 = 0.

4) Problemi i zbërthimit radioaktiv.

Le të jetë N(0) numri fillestar i atomeve të një lënde radioaktive dhe N(t) numri i atomeve të pazbërthyera në kohën t. Është vërtetuar eksperimentalisht se shpejtësia e ndryshimit të numrit të këtyre atomeve N"(t) është proporcionale me N(t), domethënë, N"(t)=–l N(t), l >0 është konstanta e radioaktivitetit të një lënde të caktuar. Në kursin shkollor të analizës matematikore tregohet se zgjidhja e këtij ekuacioni diferencial ka formën N(t) = N(0)e –l t. Koha T gjatë së cilës numri i atomeve fillestare është përgjysmuar quhet gjysmë jeta dhe është një karakteristikë e rëndësishme e radioaktivitetit të një substance. Për të përcaktuar T, duhet të vendosim formulën Pastaj Për shembull, për radonin l = 2,084 · 10 -6, dhe për këtë arsye T = 3,15 ditë.

5) Problemi i shitësit udhëtues.

Një shitës udhëtues që jeton në qytetin A 1 duhet të vizitojë qytetet A 2 , A 3 dhe A 4 , secilin qytet saktësisht një herë dhe më pas të kthehet në A 1 . Dihet se të gjitha qytetet janë të lidhura në çifte me rrugë, dhe gjatësia e rrugëve b ij ndërmjet qyteteve A i dhe A j (i, j = 1, 2, 3, 4) janë si më poshtë:

b 12 = 30, b 14 = 20, b 23 = 50, b 24 = 40, b 13 = 70, b 34 = 60.

Është e nevojshme të përcaktohet rendi i vizitës së qyteteve në të cilat gjatësia e shtegut përkatës është minimale.

Le të përshkruajmë çdo qytet si një pikë në aeroplan dhe ta shënojmë me etiketën përkatëse Ai (i = 1, 2, 3, 4). Le t'i lidhim këto pika me vija të drejta: ato do të përfaqësojnë rrugët midis qyteteve. Për çdo "rrugë" ne tregojmë gjatësinë e saj në kilometra (Fig. 2). Rezultati është një grafik - një objekt matematikor i përbërë nga një grup i caktuar pikash në aeroplan (të quajtura kulme) dhe një grup i caktuar vijash që lidhin këto pika (të quajtura skaje). Për më tepër, ky grafik është etiketuar, pasi kulmeve dhe skajeve të tij u janë caktuar disa etiketa - numra (skajet) ose simbolet (kulmet). Një cikël në një grafik është një sekuencë kulmesh V 1 , V 2 , ..., V k , V 1 e tillë që kulmet V 1 , ..., V k janë të ndryshme dhe çdo çift kulmesh V i , V i+1 (i = 1, ..., k – 1) dhe çifti V 1, V k lidhen me një buzë. Kështu, problemi në shqyrtim është gjetja e një cikli në grafik që kalon nëpër të katër kulmet për të cilat shuma e të gjitha peshave të skajeve është minimale. Le të kërkojmë nëpër të gjitha ciklet e ndryshme që kalojnë nëpër katër kulme dhe duke filluar nga A 1:

1) A 1, A 4, A 3, A 2, A 1;
2) A 1, A 3, A 2, A 4, A 1;
3) A 1, A 3, A 4, A 2, A 1.

Le të gjejmë tani gjatësitë e këtyre cikleve (në km): L 1 = 160, L 2 = 180, L 3 = 200. Pra, rruga e gjatësisë më të shkurtër është e para.

Vini re se nëse ka n kulme në një grafik dhe të gjitha kulmet janë të lidhura në çift me anë (një graf i tillë quhet i plotë), atëherë numri i cikleve që kalojnë nëpër të gjitha kulmet është Prandaj, në rastin tonë ekzistojnë saktësisht tre cikle.

6) Problemi i gjetjes së një lidhjeje midis strukturës dhe vetive të substancave.

Le të shohim disa komponime kimike të quajtura alkane normale. Ato përbëhen nga n atome karboni dhe n + 2 atome hidrogjeni (n = 1, 2 ...), të ndërlidhura siç tregohet në figurën 3 për n = 3. Le të dihen vlerat eksperimentale të pikave të vlimit të këtyre përbërjeve:

y e (3) = – 42°, y e (4) = 0°, y e (5) = 28°, y e (6) = 69°.

Kërkohet të gjendet një marrëdhënie e përafërt midis pikës së vlimit dhe numrit n për këto përbërje. Le të supozojmë se kjo varësi ka formën

y" a n+b,

Ku a, b - konstante që do të përcaktohen. Per te gjetur a dhe b ne zëvendësojmë në këtë formulë në mënyrë sekuenciale n = 3, 4, 5, 6 dhe vlerat përkatëse të pikave të vlimit. Ne kemi:

– 42 » 3 a+ b, 0 » 4 a+ b, 28 » 5 a+ b, 69 » 6 a+ b.

Për të përcaktuar më të mirën a dhe b ka shumë metoda të ndryshme. Le të përdorim më të thjeshtat prej tyre. Le të shprehemi b përmes a nga këto ekuacione:

b » – 42 – 3 a, b " – 4 a, b » 28 – 5 a, b » 69 – 6 a.

Le të marrim mesataren aritmetike të këtyre vlerave si b të dëshiruar, domethënë vendosim b » 16 - 4,5 a. Le ta zëvendësojmë këtë vlerë të b në sistemin origjinal të ekuacioneve dhe, duke llogaritur a, marrim për a vlerat e mëposhtme: a» 37, a» 28, a» 28, a" 36. Le të marrim si kërkohet a vlera mesatare e këtyre numrave, pra le të vendosim a" 34. Pra, ekuacioni i kërkuar ka formën

y » 34n – 139.

Le të kontrollojmë saktësinë e modelit në katër përbërjet origjinale, për të cilat ne llogarisim pikat e vlimit duke përdorur formulën që rezulton:

y р (3) = – 37°, y р (4) = – 3°, y р (5) = 31°, y р (6) = 65°.

Kështu, gabimi në llogaritjen e kësaj vetie për këto komponime nuk i kalon 5°. Ne përdorim ekuacionin që rezulton për të llogaritur pikën e vlimit të një përbërjeje me n = 7, e cila nuk është përfshirë në grupin origjinal, për të cilën ne zëvendësojmë n = 7 në këtë ekuacion: y р (7) = 99°. Rezultati ishte mjaft i saktë: dihet se vlera eksperimentale e pikës së vlimit y e (7) = 98°.

7) Problemi i përcaktimit të besueshmërisë së një qarku elektrik.

Këtu do të shikojmë një shembull të një modeli probabilistik. Së pari, ne paraqesim disa informacione nga teoria e probabilitetit - një disiplinë matematikore që studion modelet e fenomeneve të rastësishme të vëzhguara gjatë përsëritjes së përsëritur të eksperimenteve. Le ta quajmë një ngjarje të rastësishme A një rezultat të mundshëm të ndonjë eksperimenti. Ngjarjet A 1, ..., A k formojnë një grup të plotë nëse njëra prej tyre ndodh domosdoshmërisht si rezultat i eksperimentit. Ngjarjet quhen të papajtueshme nëse nuk mund të ndodhin njëkohësisht në një përvojë. Le të ndodhë ngjarja A m herë gjatë një përsëritjeje n-fish të eksperimentit. Frekuenca e ngjarjes A është numri W = . Natyrisht, vlera e W nuk mund të parashikohet me saktësi derisa të kryhen një seri n eksperimentesh. Megjithatë, natyra e ngjarjeve të rastësishme është e tillë që në praktikë ndonjëherë vërehet efekti i mëposhtëm: me rritjen e numrit të eksperimenteve, vlera praktikisht pushon së qeni e rastësishme dhe stabilizohet rreth një numri jo të rastësishëm P(A), i quajtur probabiliteti i ngjarja A. Për një ngjarje të pamundur (që nuk ndodh kurrë në një eksperiment) P(A)=0, dhe për një ngjarje të besueshme (që ndodh gjithmonë në përvojë) P(A)=1. Nëse ngjarjet A 1 , ..., A k formojnë një grup të plotë ngjarjesh të papajtueshme, atëherë P(A 1)+...+P(A k)=1.

Për shembull, eksperimenti konsiston në hedhjen e një zari dhe vëzhgimin e numrit të pikave të hedhura X Më pas mund të prezantojmë ngjarjet e rastësishme të mëposhtme A i = (X = i), i = 1, ..., 6. Ato. formojnë një grup të plotë të ngjarjeve të papajtueshme po aq të mundshme, prandaj P(A i) = (i = 1, ..., 6).

Shuma e ngjarjeve A dhe B është ngjarja A + B, e cila konsiston në faktin se të paktën njëra prej tyre ndodh në përvojë. Produkti i ngjarjeve A dhe B është ngjarja AB, e cila përbëhet nga ndodhja e njëkohshme e këtyre ngjarjeve. Për ngjarjet e pavarura A dhe B, formulat e mëposhtme janë të vërteta:

P(AB) = P(A) P(B), P(A + B) = P(A) + P(B).

8) Le të shqyrtojmë tani sa vijon detyrë. Le të supozojmë se tre elementë janë të lidhur në seri me një qark elektrik dhe funksionojnë në mënyrë të pavarur nga njëri-tjetri. Probabilitetet e dështimit të elementeve 1, 2 dhe 3 janë përkatësisht të barabarta me P1 = 0,1, P2 = 0,15, P3 = 0,2. Ne do ta konsiderojmë një qark të besueshëm nëse probabiliteti që nuk do të ketë rrymë në qark nuk është më shumë se 0.4. Është e nevojshme të përcaktohet nëse një qark i caktuar është i besueshëm.

Meqenëse elementët janë të lidhur në seri, nuk do të ketë rrymë në qark (ngjarja A) nëse të paktën një nga elementët dështon. Le të jetë A i ngjarja që funksionon elementi i-të (i = 1, 2, 3). Pastaj P(A1) = 0,9, P(A2) = 0,85, P(A3) = 0,8. Natyrisht, A 1 A 2 A 3 është një ngjarje në të cilën të tre elementët punojnë njëkohësisht, dhe

P(A 1 A 2 A 3) = P(A 1) P(A 2) P(A 3) = 0,612.

Atëherë P(A) + P(A 1 A 2 A 3) = 1, pra P(A) = 0,388< 0,4. Следовательно, цепь является надежной.

Si përfundim, vërejmë se shembujt e dhënë të modeleve matematikore (përfshirë funksionale dhe strukturore, përcaktuese dhe probabiliste) janë natyrë ilustruese dhe, padyshim, nuk shterojnë shumëllojshmërinë e modeleve matematikore që dalin në shkencat natyrore dhe shkencat humane.